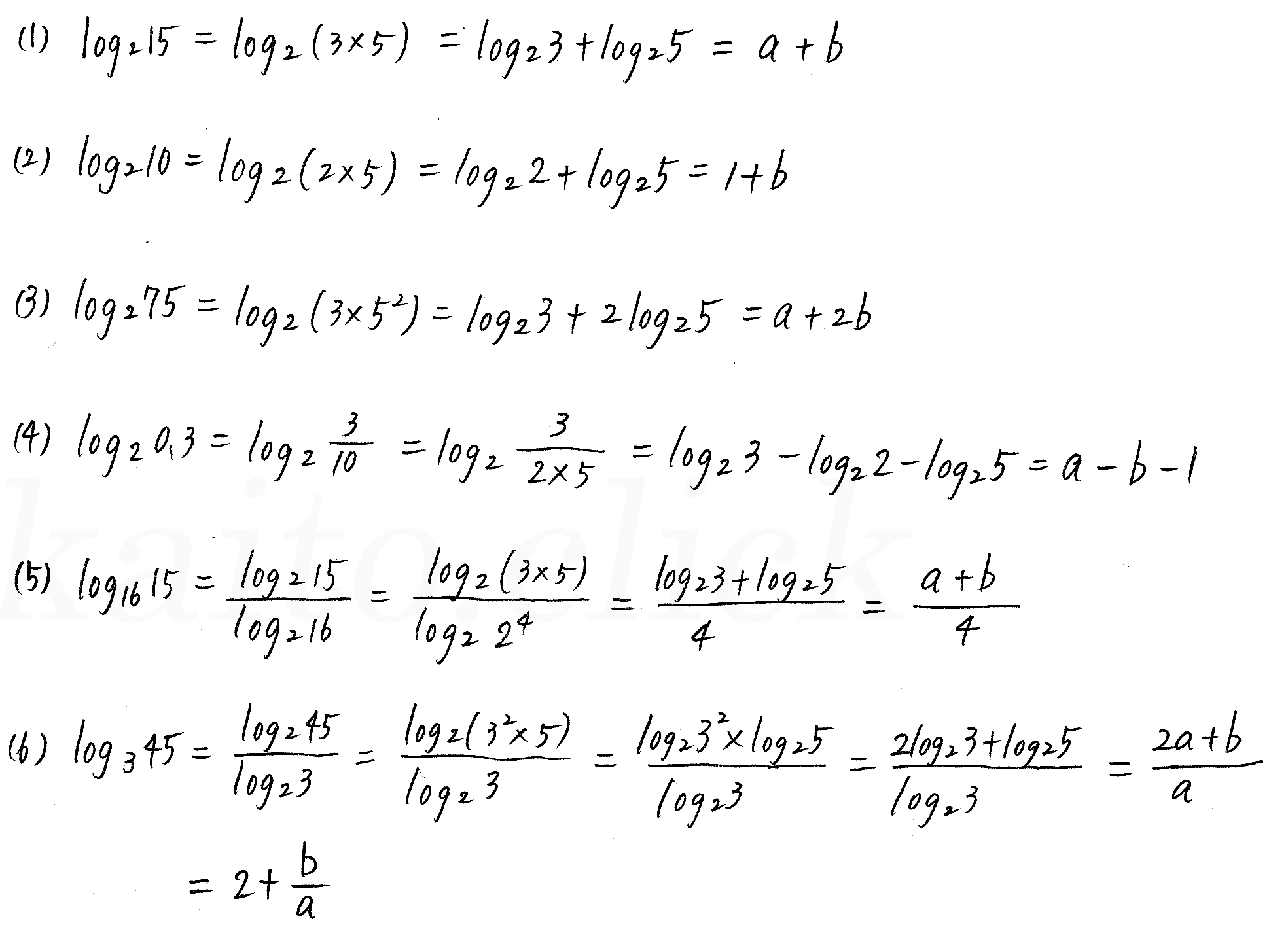対数 と その 性質. 対数正規分布 λ(μ 1, σ 1 2) に従う確率変数 x と対数正規分布 λ(μ 2, σ 2 2) に従う確率変数 y が互いに独立であるとき、確率変数の積 xy は対数正規分布 λ(μ 1 + μ 2, σ 1 2 + σ 2 2) に従う。 この性質は正規分布が再生性を有することから導かれる。 中心極限定理. 先ほど書いたように、対数には「0 < a < 1」という性質がありますので、面倒です。 よって、 底を1より大きい値に変換 してしまいましょう。 このときに用いるのが、 底の変換.
クリアー数学Ⅱ(数2) P74 31 対数とその性質 from kaito.click
これは、(ア) 底と真数が同じ値ならばその対数は1となる性質 と、(イ) 真数の指数はlogの前に出すことができる性質 を利用したものです。 (ア)の例を挙げるとlog 2 2=1となります。 どんな数を1乗しても値は変わりませんから当然ですね。 対数正規分布 λ(μ 1, σ 1 2) に従う確率変数 x と対数正規分布 λ(μ 2, σ 2 2) に従う確率変数 y が互いに独立であるとき、確率変数の積 xy は対数正規分布 λ(μ 1 + μ 2, σ 1 2 + σ 2 2) に従う。 この性質は正規分布が再生性を有することから導かれる。 中心極限定理. 先ほど書いたように、対数には「0 < a < 1」という性質がありますので、面倒です。 よって、 底を1より大きい値に変換 してしまいましょう。 このときに用いるのが、 底の変換.
クリアー数学Ⅱ(数2) P74 31 対数とその性質
これは、(ア) 底と真数が同じ値ならばその対数は1となる性質 と、(イ) 真数の指数はlogの前に出すことができる性質 を利用したものです。 (ア)の例を挙げるとlog 2 2=1となります。 どんな数を1乗しても値は変わりませんから当然ですね。 これは、(ア) 底と真数が同じ値ならばその対数は1となる性質 と、(イ) 真数の指数はlogの前に出すことができる性質 を利用したものです。 (ア)の例を挙げるとlog 2 2=1となります。 どんな数を1乗しても値は変わりませんから当然ですね。 先ほど書いたように、対数には「0 < a < 1」という性質がありますので、面倒です。 よって、 底を1より大きい値に変換 してしまいましょう。 このときに用いるのが、 底の変換. 対数正規分布 λ(μ 1, σ 1 2) に従う確率変数 x と対数正規分布 λ(μ 2, σ 2 2) に従う確率変数 y が互いに独立であるとき、確率変数の積 xy は対数正規分布 λ(μ 1 + μ 2, σ 1 2 + σ 2 2) に従う。 この性質は正規分布が再生性を有することから導かれる。 中心極限定理.
