平行 線 と 線 分 の 比 応用 問題. 平行線と線分の比 平行線と線分の比の問題です。 基本をしっかりおさえていれば、点数が取りやすい単元です。 比を取る線分に注意をして確実に出来るようにしてください。 比例式の計算を出来るようにしておきましょう 比例式の計算が必要になします。 比例式の解き方 の「内項の積＝外項の積」を使って解けるようにします。 ＊ただし、暗算で出来る、倍. 平行線と線分の比下の図で、直線 \(l,m,n\) が平行ならば、線分の長さの比について以下のことが成りたつ。 \(ab:bc = de:ef\) これはなぜ成り立つのか。下の図のように、\(df\) と平行な線分 \(ah\) を引けば、ピラミッド型相似ができます。
最高かつ最も包括的な三角形 辺の比 定理 ただぬりえ from blogambaredudisipjp.blogspot.com
Step $\textcolor{blue}{1}$ ： $\textcolor{blue}{\rm abe∽ dce}$ $\rm ab:dc=9cm:12cm=\textcolor{blue}{3:4}$ (相似比) point：対応する線分の長さの比は、すべて等. 平行線で区切られた線分の比の定理 「平行線と比の定理」の 型と 型は、台形のようなものにも応用できますね！ 直線 t を平行移動させた t’ も、 当然 a’：b’ ですね！ (t と t’ の間の空間は平行四辺形) 実は、3本の平行線(に交わる直線の「 比 」は. 平行線と線分の比 \(2\) つの図形において、いくつかの辺の長さがわかっているとき、長さがわからない辺の長さを求めるために平行線の定義を利用することがあります。 証 明
最高かつ最も包括的な三角形 辺の比 定理 ただぬりえ
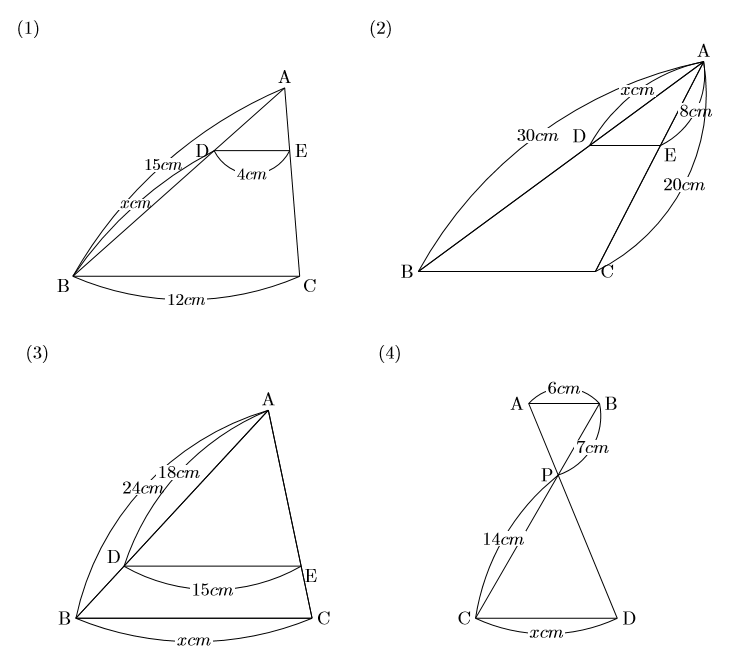
次の図で、直線 \(l,m,n\) が平行のとき、\(x\) の値を求めなさい。 ①. 【fddata 中間期末：中学数学3 年：平行線】 [三角形と線分の比／平行線にはさまれた線分の比／平行線と線分比応用／ 三角形の角の二等分線と線分の比 ／中点連結定理：証明問題／長さ・角度の計算／全般／ fddata 中間期末製品版のご案内] 平行線と線分の比 平行線と線分の比の問題です。 基本をしっかりおさえていれば、点数が取りやすい単元です。 比を取る線分に注意をして確実に出来るようにしてください。 比例式の計算を出来るようにしておきましょう 比例式の計算が必要になします。 比例式の解き方 の「内項の積＝外項の積」を使って解けるようにします。 ＊ただし、暗算で出来る、倍. よく使う相似の形。 afの延長線とdcの延長線の交点をhとする。 するとab//cdから abf∽ hcfとなる。 bf:fc=2:1なので相似比は2:1である abとhcが対応する辺なので ab=4とするとhc=2となる。 また、ab//cdから aeg∽ hdgとなる。 ab=4ならcd=4なのでhd=6 よってae:hd=1:6
